Contact mechanics is the study of the deformation of two solids that come into contact. It is fundamental to the field of mechanical engineering by providing information necessary for the safe and energy efficient design of technical systems. Much research has been carried out in the last decades to find accurate contact mechanics models. However a full comprehension of the nature of the contact between two solids with randomly rough surfaces has been achieved only recently. The complication here is that surfaces of solids usually exhibit surface roughness over many decades in length scales. In general, when two elastic solids with surface roughness are squeezed together, they do not make contact everywhere in the apparent contact area. Only at a distribution of asperity contact spots, real atomic contact exists.
Practically all macroscopic bodies in Nature and technology have surfaces with roughness on many different length scales. Even a highly polished surfaces, appearing perfectly smooth to the naked eye, exerts small scale surface roughness when increasing the magnification looking at the surface. This is for example true for the extremely well polished rolling elements from a ball bearing shown below. Within an approach to this problem one should always take into account all length scale roughness components in order to not neglect any important contribution! In the context of contact mechanics the three most important physical quantities are the area of real contact, the interfacial separation in the non-contact regions, and the stress distribution in the contact regions
 |
| Rolling elements from a ball bearing which appear extremely smooth to the naked eye. However at high enough magnification one will find surface roughness even on those surfaces. |
The figure below illustrates that contact mechanics is a multiscale problem where all surface roughness components, starting maybe at cm scale and ending at atomic dimensions, need to be described in an appropriate way. When two bodies with nominally flat surfaces are brought into contact, real (atomic) contact will only occur in small randomly distributed areas, thus the area of real contact is usually an extremely small fraction of the nominal contact area.
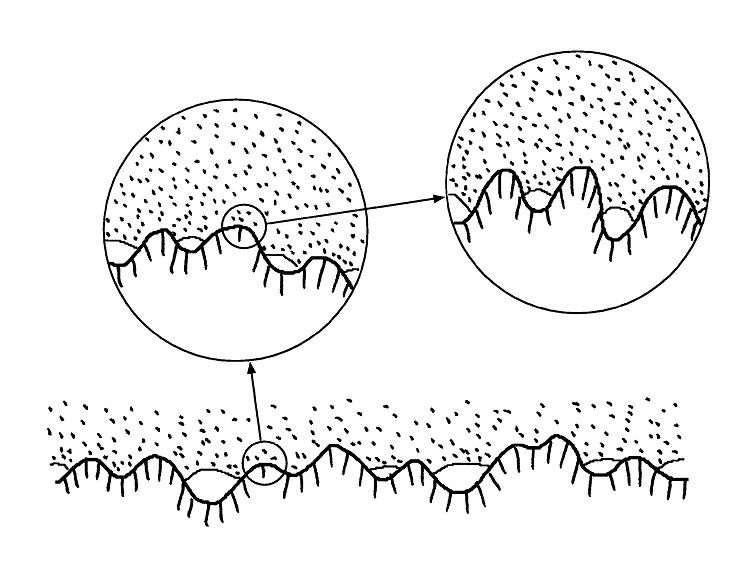 |
| A rubber block (dotted area) in contact with a hard rough substrate (dashed area). The substrate has roughness on many different length scales and the rubber makes partial contact with the substrate on all length scales. When a contact area is studied at low magnification(zeta = 1) it appears as if complete contact occurs in the macro-asperity contact regions, but when the magnification is increased it is observed that in reality only partial contact occurs. |
The consequence of this is that any approach towards contact mechanics has to take into account roughness on different length scales. When describing the contact between a car tire with the road, the roughness components may vary from centimetre range (size of the largest stone particles the road consists of) all the way down to atomic resolution. This means the approach has to be able to handle more than 7 decades in roughness length scales. Because of the limited computer resources this problem cannot be studied numerically. There are simply too many degrees of freedom involved so that even with modern supercomputer the calculation could not be solved within a sufficient time period. The consequence is, that an analytical approach is needed to understand contact mechanics.
Contact mechanics has a long history also because of its importance for numerous processes in Nature and technology. How large is the area of real contact between a solid block and a substrate? This fundamental question has extremely important practical implications. For example, it determines the contact resistivity and the heat transfer between two solids. It is also of direct importance for wear and sliding friction, e.g., the rubber friction between a tire and a road surface, and has a major influence on the adhesive force between two solid blocks in direct contact. The true contact area as well as the size of the gap between two solids are of crucial importance for seals and for the optical properties of composite systems, e.g., the optical interference between glass lenses. The most important questions addressed by contact mechanics are:
|
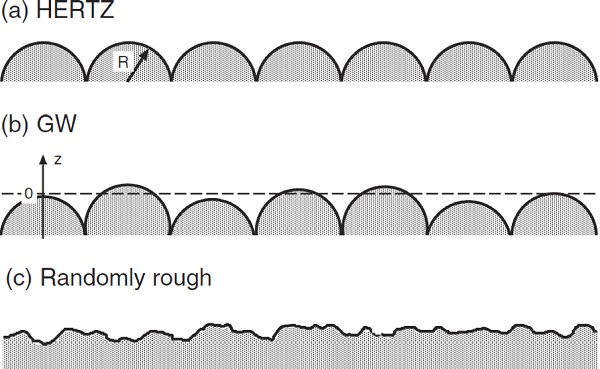 |
| Three different models of a “rough” surface. In case (a) all the asperities are equally high and have identical radius of curvature. Introducing asperities with a random height distribution as in (b) gives the Greenwood-Williamson approach on contact mechanics. In (c) a real, randomly rough surface is shown where the asperities are of different heights and curvature radii. |

Recently a novel and fundamentally different approach towards contact mechanics has been presented by Persson. In contrast to the multiasperity contact theories, where the area of real contact has to be much smaller than the nominal contact area, this approach starts from the opposite limit of very large contact. Here the squeezing force is so high that nearly complete contact occurs, and in this limit the theory predictions are exact. For small forces the projected (on the xy-plane) contact area A is proportional to the load Fn, while A approaches A0 in a continuous manner as Fn increases towards infinity. In this theory a diffusion-like equation is used to calculate the stress distribution at the interface. This equation is derived by studying the interface at different magnification zeta. First the surface is considered to be smooth with no noticeable roughness. Looking at the interface with low magnification (or low resolution), no surface height variations can be observed. The surface appears perfectly smooth. The magnification is then successively increased so that more and more (or shorter and shorter) roughness components are considered. Including all length scales gives the full stress distribution observed at the highest magnification. The area of real contact can then be deduced from the stress distribution.
The theory needs as input the surface roughness power spectrum C(q) and the elastic properties E and Poisson's ration nu of the two contacting bodies. P(sigma, zeta) is the stress distribution in the contact areas under the magnification zeta. It satisfies the following differential equation:
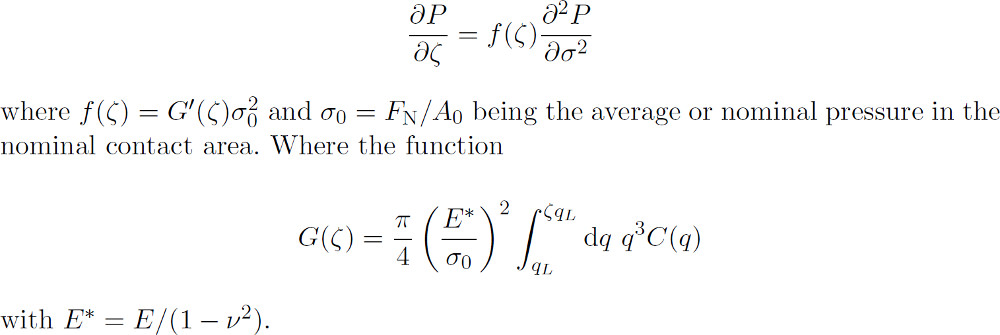
The first equation is a diffusion-like equation where time is replaced by magnification zeta, the spatial coordinate with the stress sigma and where the “diffusion constant” f(zeta) depends on zeta. The physical meaning of the equation is the following. Studying a system at the lowest magnification zeta = 1 no surface roughness can be observed and the block makes (apparent) contact with the substrate everywhere in the nominal contact area, see figure below (a) left. For this case, if friction at the interface can be neglected, the stress at the interface equals everywhere the applied stress sigma0, and the stress distribution ((a) right) is a delta function P(sigma, 1) = delta (sigma - sigma0). Increasing the magnification, surface roughness with wavelength down to lambda = L/zeta is introduced to the system leading to emerging non-contact regions. Since the stress must continuously go to zero at the edges of the boundary between the contact and the non-contact regions (like in the Hertz theory), it follows that the stress distribution P(sigma, zeta) exhibits a tail extending the whole way down to zero stress as indicated in (b). There will also be a tail towards larger stresses sigma <> sigma0 because the average stress must be equal to sigma0. With increasing magnification this distribution broadens more and more like in a diffusion problem, as indicated in (c).
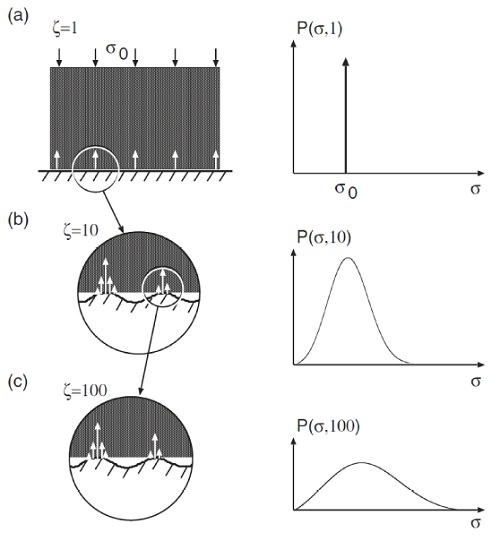 |
| The stress distribution in the contact region between a rigid block and an elastic substrate at increasing magnification zeta. At the lowest magnification zeta = 1 the substrate looks smooth and the block makes apparent contact with the substrate in the whole nominal contact area leading to a delta function in the stress distribution. As the magnification increases the area of contact decreases while the stress distribution becomes broader and broader. |
The expression for the stress distribution P(sigma, zeta) at the interface when the contact is studied at the magnification zeta = L/lambda, where lambda is the shortest surface roughness wavelength which can be detected at the resolution zeta, can be written as
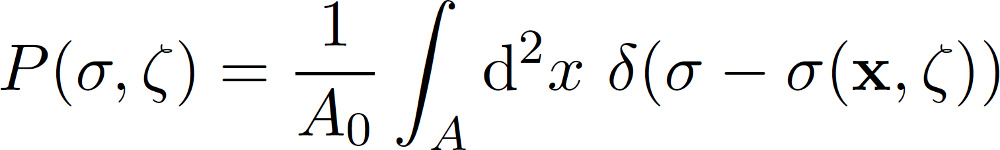
with sigma(x, zeta) being the stress at the interface when only the surface roughness components with wavevector q < zeta * qL is considered. The integral in the equation above is performed over the area of contact A. Integrating over the whole surface area A0, the stress probability function would have a delta function [(A0 - A) / A0] delta(sigma). However this is excluded in this approach. From the stress distribution it is possible to directly obtain the area of real contact projected on the xy-plane. It follows that
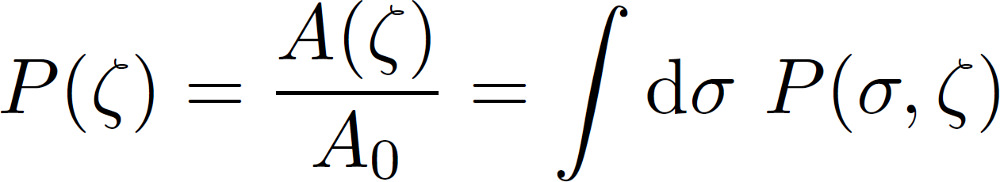
The equation for P(sigma, zeta) satisfies the diffusion-like equation shown above assuming complete contact. With some appropriate boundary conditions and assuming that the equation holds locally also when only partial contact occurs, the area of (apparent) contact can be derived as follows
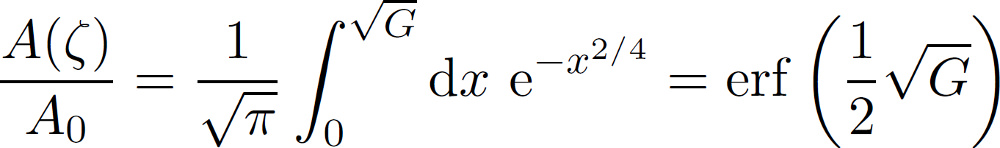
where G(zeta) has been given already above. With the help of this equation the area of contact can be calculated for a particular magnification. If the power spectrum has been measured down to atomic resolution it is possible with the help of this approach to calculate the true area of contact at atomic resolution. Also the stress probability distribution can be calculated as explained already above. To learn more about the approach we would like to refer you to our online library where a lot of publications on the theory can be found. Note that this approach on contact mechanics has been tested both experimentally and using numerical studies. So far the agreement was very good showing that the basic theory is correct. Based on the theory of Persson we at Multiscale Consulting have applied this approach to many different topics. The theory as it exists today is robust and exact.
 |
| Pictures of a rubber sample forming contact and penetrating into the surface roughness valleys with increasing normal pressure. The dark area is where the rubber is in contact with the substrate. |
In case you want to learn more about the validation of the theory please visit our validation section. The codes which have been written during the development of the approach is also available as software.
If you are interested in using the contact mechanics program or you have further questions concerning the theory please feel free to contact us.
